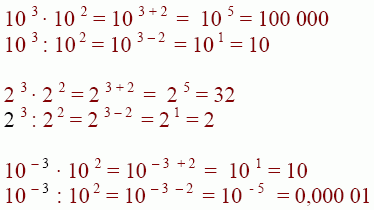Potenzen
Etwas über Potenzen
Bereits den Babyloniern (ca. 3 500 v. Chr.) waren Tabellen von Quadratzahlen und Potenzen bekannt und sie verstanden es Zinseszinsaufgaben mit Hilfe von Zweierpotenzen zu lösen.
Natürlich 6 ∙ 2 = 12. Oder einfach zusammenzählen.
Wie würden Sie 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2
oder 10 ∙ 10 ∙ 10 ∙ 10
oder x ∙ x ∙ x ∙ x ∙ x schreiben?
In der Mathematik gibt es dafür eine abkürzende und Platz sparende Schreibweise, nämlich die Potenzschreibweise.
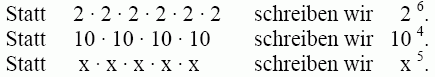
Wir sagen zu der Potenz 
zwei hoch sechs und nennen die 2 Basis oder Grundzahl und die 6 Hochzahl oder Exponent.
Eine Besonderheit ist es, wenn die Hochzahl 0 ist.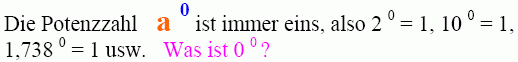
10-er Potenzen
Da wir uns meist im Dezimalsystem bewegen, sei hier auf die 10-er Potenzen eingegangen.
Jede Dezimalzahl können wir als Kommazahl mit 10-er Potenz schreiben.
Verschieben wir das Komma um eine bestimmte Anzahl Stellen nach links, erhöht sich die Hochzahl (Exponent) um dieselbe Anzahl.
(Klar, verschieben wir das Komma eine Stelle nach links erniedrigt sich der Zahlenwert um eine zehner Potenz und mit der um eins erhöhten Potenz gleichen wir das wieder aus.)
Verschieben wir das Komma um eine bestimmte Anzahl Stellen nach rechts, erniedrigt sich die Hochzahl (Exponent) um dieselbe Anzahl.
(Klar, der Zahlenwert erhöht sich, wenn wir das Komma nach rechts verschieben und mit der erniedrigten Potenz gleichen wir das wieder aus.)
Beispiel:
Große Zahlen
Wollen wir eine lange oder große Dezimalzahl in Potenzschreibweise umformen, brauchen wir nur das Komma nach links zu verschieben und die Anzahl der Verschiebungen ergibt den Wert der Hochzahl der Zehner-Potenz.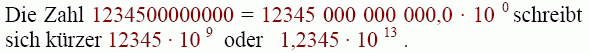
Umgekehrt bekommen wir wieder eine Dezimalzahl, wenn wir entsprechend dem Wert der Hochzahl das Komma nach rechts verschieben.
km
Kleine Zahlen
Der Wert der Hochzahl ist entsprechend der Anzahl der Nachkommastellen – 9.
Die Masse eines Elektrons beträgt etwa
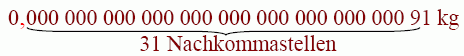
Würden Physiker immer so schreiben müssen, würden sie verzweifeln. In Potenzschreibweise lautet die Zahl 
Multiplikation und Division von Potenzen
Potenzen mit gleicher Basis können sowohl multipliziert wie auch dividiert werden. Das machen wir uns an Hand der zehner Potenzen klar.
Multiplikation:
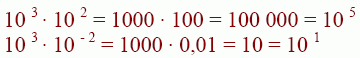
Wir sehen, Potenzen mit gleicher Basis multiplizieren wir, indem wir ihre Hochzahlen (Exponenten) zusammenzählen.
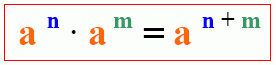
Division:
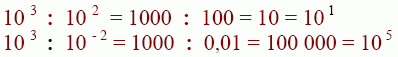
Wir sehen, Potenzen mit gleicher Basis dividieren wir, indem wir ihre Hochzahlen (Exponenten) voneinander abziehen.
Allgemein gilt: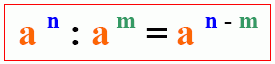 
Beispiele:
