Beispiele zur Proportion (Verhältnisgleichung)
Geben Sie das Verhältnis der Größe eines Elefanten (260 cm) im
Verhältnis zur Größe einer Maus (4 cm) in Prozent an.
Elefant : 260 cm entspricht 100 %
Maus : 4 cm entspricht x %
Verhältnisgleichung: 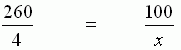
Gleichung durch 260 teilen
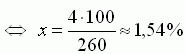
Die Größe der Maus beträgt also rund 1,5 % im Vergleich zur Größe eines Elefanten.
(Das Zeichen <=> bedeutet „äquivalent“ oder „gleichbedeutend mit“)
Vierstreckensatz
Eine fundamentale und wichtige Anwendung einer Verhältnisgleichung in der Mathematik ist der so genannte Vierstreckensatz. Weil dieser Satz, nicht nur im Zusammenhang mit unserem Thema, wichtig ist, möchte ich ihn hier eigens vorstellen.
Zwei Dreiecke sind ähnlich, wenn ihre Winkel gleich sind. Dann nämlich ist das eine Dreieck nur eine Vergrößerung oder Verkleinerung des anderen Dreiecks. In dem besonderen Fall, dass beide Dreiecke gleich sind, sprechen wir von deckungsgleich oder kongruent. Interessant ist nun, dass bei ähnlichen Dreiecken die Verhältniszahlen zweier entsprechender Seiten gleich sind. Es gilt also a : b = a* : b* oder c : b = c* : b* oder a : c = a* : c* usw.
Animation Vierstreckensatz
In der Geometrie haben wir es oft mit ähnlichen Dreiecken zu tun, und der Vierstreckensatz ist ein ideales mathematisches Werkzeug bei geometrischen Konstruktionen und Konstruktionsbeweisen.
Der Goldene Schnitt
Wenn wir die Strecke AB (in der Mathematik schreiben wir Strecken mit einem Deck-Strich) zu 1 machen, was wir hier dürfen, da wir die Strecke ja eh willkürlich gewählt haben und den Major (blau) als x bezeichnen, ist der Minor (grün) 1 – x (s. Abb. unten). Die Gleichung vereinfacht sich dann erheblich.
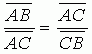 .
.
Damit haben wir erreicht, dass wir nur noch eine unbekannte Größe in der Verhältnisgleichung haben. Dieses x werden wir in der folgenden Kurseinheit 2 bestimmen.
Und noch ein imposantes Beispiel.
Proportion als ein Transformationswerkzeug.
Über die Größenverhältnisse im Weltall machen wir uns kaum eine richtige Vorstellung, zu groß sind die Zahlen mit denen wir es da zu tun haben. Dasselbe gilt für die Verhältnisse im Mikrokosmos. Da tun wir gut daran, wenn wir die riesigen Zahlenverhältnisse auf einen für uns verträglichen Maßstab transformieren.
Angenommen die Sonne hätte die Größe eines Fußballs, wie wären dann die Größenverhältnisse in Bezug auf die Erde oder anders gefragt, wie groß wäre dann die Erde und welchen Abstand hätte sie vom Fußball?
Hier ein paar Daten:
Durchmesser der Sonne 1,4·10^6 km
Durchmesser der Erde 1,27·10^4 km
Durchmesser des Fußballs 0,2 m
mittlere Entfernung Sonne − Erde 1,5·10^8 km
Tipps: Stellen Sie eine entsprechende Verhältnisgleichung auf.
10^2 (10 hoch 2) bedeutet 10 mal 10 also 100 entsprechend bedeutet
10^3 = 10 mal 10 mal 10 = 1000 usw. s.a. Potenzen
Animierter Lösungsvorschlag Größenverhältnis
Lösungsvorschlag Abstand
Leonardo da Vincis Proportionsskizze