Verhältnis
Was ist ein Verhältnis? Wir sprechen ganz praktisch von Straßenverhältnissen, Schneeverhältnissen oder sagen auch jemand habe ein gutes oder schlechtes Verhältnis zu jemand oder zu irgendetwas. Wenn wir so sprechen, vergleichen wir zwei unterschiedliche Zustände, Qualitäten (Eigenschaften) oder Quantitäten (Mengen) und setzen sie in ein Verhältnis. Eine Maus ist zum Beispiel im Verhältnis zu einem Elefanten sehr klein. Dieses Verhältnis können wir durch ein Zahlenverhältnis ausdrücken.
Größe der Maus zur Größe des Elefanten , also etwa 4 cm zu 260 cm.

Mathematisch schreiben wir: 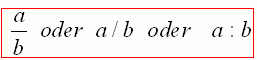
Für unser Beispiel oben erhalten wir dann das Verhältnis: 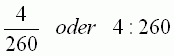

Ein Verhältnis oder ein Vergleich ist der Quotient zweier Größen. Allgemein gesprochen bildet ein Verhältnis die Grundlage für alle Wahrnehmungsprozesse und ist somit ein Basis-Prozess für begriffliches Urteilen, für Intelligenz.
Aufgepasst!
Auch wenn das Zeichen „ : “ wie ein Bruchstrich oder als ein „geteilt“-Zeichen verwendet wird, gibt es noch einen Unterschied zwischen der Bruch-Schreibweise und der Doppelpunkt-Schreibweise.
Der Bruch ¾ bedeutet 3 Teile eines in 4 Teile geteilten Ganzen.
Beispiel: Ein Kuchen wird in vier Teile geteilt. Sie bekommen ¼ davon, ich bekomme ¾ davon.
Das Verhältnis 3 : 4 bedeutet 3 Teile und 4 Teile eines in 7 Teile geteilten Ganzen.
Beispiel: 3 Liter Saft und 4 Liter Wasser ergeben 7 Liter Mischgetränk. Saft und Wasser stehen im Verhältnis 3 : 4.
Der Saftanteil beträgt also 3/7 und der Wasseranteil 4/7.
Das Symbol „ : “ wurde erstmals von dem britischen Mathematiker William Oughtred (1575 – 1660) verwendet.
Beispiel:
Das Verhältnis von Umfang zu Durchmesser eines Kreises ist für alle Kreise gleich.Oder anders gesagt, der Umfang eines Kreises ist dreimal der Durchmesser des Kreises plus ein bisschen.
Das ist natürlich sehr praktisch.
Wenn wir den Umfang eines Kreises bestimmen wollen, ist es einfacher den Durchmesser mit Hilfe eines Lineals oder Meterstabs zu bestimmen, als den Umfang. Multiplizieren wir dann den Durchmesser mit 3,14 erhalten wir den Umfang.
Wollen wir dagegen den Durchmesser eines imposanten Baumes bestimmen, messen wir den Umfang und teilen diesen durch 3,14.